Reasons Why we Round off Numbers: Mathematics Lesson

Reasons Why we Round off Numbers: Mathematics Lesson Rounding numbers maintains the number’s original value while also making them “easier” to use or comprehend. Simpler values may be used in place of exact integers.

189.2 might be rounded to 189, 190, or 200, for instance, depending on the level of precision needed. In this case, £19.99 may be rounded to £20 and 56 minutes to an hour.

Rounding to the nearest 10

Pupils first officially encounter this in Year 4. In order to round to the nearest 10, children must first understand what multiples of ten are (numbers in the ten times table, or numbers divisible by 10, e.g. 30, 250, 3430 etc.).

They must then be able to identify which multiples of 10 a given number is between, e.g. 218 is between 210 and 220 (a number line is often used for this, as seen below).

Finally, children should then identify the nearest multiple of 10 – in this case, 220. Children should round numbers up If they lie halfway between two multiples (and therefore end in a 5).

In this case the number will always round up to the multiple of 10 above it.

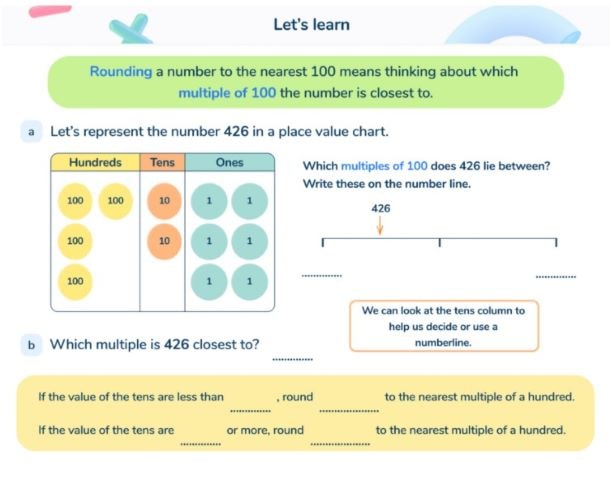
Rounding to the nearest 100

Pupils first officially encounter this in Year 4. In order to round to the nearest 100, children must first understand what multiples of 100 are (numbers in the 100 times table, or numbers divisible by 100, e.g. 500, 2500, 34300 etc.).

They must then be able to identify which multiples of 100 a given number is between, e.g. 218 is between 200 and 300 (a number line is often used for this).

Finally, children should then identify the nearest multiple of 100 – in this case, 200. If a number lies halfway between (and therefore ends in 50), the number will always round up to the multiple of 100 above it.

Rounding to the nearest whole number

Pupils first officially encounter this in Year 4. Children must be able to identify which whole numbers, also termed ‘integers’, are either side of a decimal number.

For example, 6.2 is between 6 and 7; 14.92 is between 14 and 15 (again, a number line is a useful tool in helping to visualise this).

They should then work out which of these integers is closer to the decimal number using the numbers to the right of the decimal point.

As before, if the decimal number is exactly halfway between two integers (such as 3.5), it will always round up to the integer above it (in this case, 4).

Rounding to the nearest tenth

Pupils first officially encounter this in Year 5. In a similar fashion to the methods previously explained, children should be able to identify the tenths either side of a decimal number.

For example, 4.62 is between 4.6 and 4.7; 5.213 is between 5.2 and 5.3.

Sometimes these decimal numbers could be written with a 0 in the hundredths place and/or thousandths place value to make it easier to work out the surrounding tenths: in the first example above, 4.62 has 62 hundredths and is therefore between 60 hundredths (4.60, or 4.6) and 70 hundredths (4.70, or 4.7).

Finally, children should then work out which of these tenths is closer to the decimal number. As the nearest hundredth of 4.62 is 60, the nearest tenth is will be 6.

Once again, if the decimal number is exactly halfway between two tenths (such as 2.75), it will always round up to the tenth above it (in this case, 2.8).

When do children learn about rounding numbers in the national curriculum?

Pupils may first encounter rounding in Year 3, where the non-statutory guidance advises that, in geometry, they could “connect decimals and rounding to drawing and measuring straight lines in centimetres, in a variety of contexts”.

However, it isn’t until Year 4 that children are required to be taught to:

• round any number to the nearest 10, 100 or 1000
• round decimals with one decimal place to the nearest whole number

This progresses to Year 5, where pupils are expected to:

• round any number up to 1 000 000 to the nearest 10, 100, 1000, 10 000 and 100 000
• round decimals with two decimal places to the nearest whole number and to one decimal place
• check answers to calculations and determine, in the context of a problem, levels of accuracy

And finally to Year 6:

• round any whole number to a required degree of accuracy
• solve problems which require answers to be rounded to specified degrees of accuracy
• interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context

How does rounding numbers relate to other areas of maths?

As often mentioned in the National Curriculum, rounding is used to estimate and check answers to problems.

For example, when multiplying decimals (such as 0.7 x 0.8), pupils may misinterpret the magnitude of the answer (in this case, perhaps 5.6).

Rounding the decimals and then multiplying (0.7 and 0.8 both round to 1, and 1 x 1 = 1) helps to check the accuracy of the answer (5.6 is much larger than 1, so the multiplication could be recalculated to achieve 0.56, which is much closer to 1).

Rounding in maths in real life

Rounding is useful in real life, most notably in measurement. For example, rounding remainders appropriate to the context:

• Rounding up: A minibus holds 12 people and you need to transport 161 people. 161 ÷ 12 = 13.4, but you can’t have 0.4 of a minibus, so you would need to round up to work out that 14 minibuses would be needed
• Rounding down: An egg box holds 12 eggs and you have 161 eggs to package. 161 ÷ 12 = 13.4, but you can’t have 0.4 of an egg-box and they all must be fully filled, so you would need to round down to work out that 13 egg boxes would be needed.

In the first example, 13.4 wouldn’t conventionally be rounded up, but in the context of the problem, it was required to be.

3 worked examples for rounding in maths

1) Round 218 to the nearest multiple of 10.

Answer: 220

2) Round 42.4 to the nearest whole number.

Answer: 42

3) Round 1.15 to the nearest tenth.

Answer: 1.2 (any number that is halfway between always rounds up)

Once children are confident with the concept through using a number line, they may be able to round by just looking at two digits:

• When rounding to the nearest 10, you only need to look at the tens place (to identify if it will change or not) and the ones place (to identify if it will round the tens digit up or down) – e.g. in 3,268, the 8 rounds the 6 ‘up’ to a 7, becoming 3,270
• When rounding to the nearest 100, you only need to look at the hundreds digit (to identify if it will change or not) and the tens digit (to identify if it will round the hundreds digit up or down) – e.g. in 742,125, the 2 rounds the 1 ‘down’ to stay as 1, becoming 742,100
• When rounding to the nearest 1000, you only need to look at the digits in the thousands and hundreds place – e.g. in 42,517, the 5 rounds the 2 ‘up’ to a 3, becoming 43,000

… and so on.

5 rounding in maths practice questions and answers

Year 4

Q: Circle the number which is closer to 1000 and explain how you know: 996, 1006

Answer: 996 is closer to 1000 as it is only 4 away, whereas 1006 is 6 away.

Year 5

Q: Round 73,482 to the nearest: a) 10,000   b) 1,000   c) 100

Answer: a) 70,000   b) 73,000 c)   73,500

Q: Round 3,593,174 to the nearest million.

Answer: 4,000,000

Year 6

Q: John thinks of a whole number. He multiplies it by 4. He rounds his answer to the nearest 10. The result is 50. Write all the possible numbers that John could have started with.

Answer: 12 or 13 (Any number from 45 – 54 would be rounded to 50 when being rounded to the nearest 10. There are only two multiples of 4 within that range: 48 and 52. Dividing those by 4 gives you 12 and 13)

Q: Round each of these numbers to the nearest 100: a) 20,906   b) 2,090.6   c) 209.06

Answer: a) 20,900   b) 2,100   c) 200