JOIN OUR WHATSAPP GROUP. CLICK HERE

Mathematics Grade 8 Probability Questions and Answers for Revision

Solution:

Total number of trials = 300 (Since there are 300 students all together).

Number of times a cricket player is chosen = 95 (Since 95 students play cricket).

Number of times a football player is chosen = 120.

Number of times a volleyball player is chosen = 80.

Number of times a student is chosen who plays no games = 5.

(i) Therefore, the probability of getting a player who plays volleyball

= $\frac{Number of Times a Volleyball Player can be Chosen}{Total Number of Trials}$

= $\frac{80}{300}$

= $\frac{4}{15}$

(ii) The probability of getting a player who plays either cricket or volleyball

= $\frac{Number of Times a Cricket or a Volleyball Player can be Chosen}{Total Number of Trials}$

= $\frac{95 + 80}{300}$

= $\frac{175}{300}$

= $\frac{7}{12}$

(iii) The probability of getting a player who plays neither football nor volleyball = $\frac{Number of Times a Student can be Chosen who do not Play Football or Volleyball}{Total Number of Trials}$

= $\frac{300 - 120 - 80}{300}$

= $\frac{100}{300}$

= $\frac{1}{3}$

2. The blood group of 60 students of a class recorded as below.

Blood Group	A	B	AB	O
Number of Students	12	20	10	18

A student of the class is selected at random.

(i) What is the probability that the selected student has blood group O?

(ii) What is the probability that the selected student does not have blood group O?

Solution:

(i) Total number of trials = 60. [Since, there are 60 different students).

Number of students having blood group O = 18.

So, the probability of the student’s blood group being O

= $\frac{Frequency of FavourableTrials}{Total Number of Trials}$

= $\frac{Number of Students having BloodGroup O}{Total Number of Trials}$

= $\frac{18}{60}$

= $\frac{3}{10}$

(ii) Total number of trials = 60. [Since, there are 60 different students).

Number of students not having blood group O = Total Number of Students – Number of Students having Blood Group O = 60 – 18 = 42.

So, the probability of the student’s blood group being different from O

= $\frac{Number of Students not havingBlood Group O}{Total Number of Trials}$

= $\frac{42}{60}$

= $\frac{7}{10}$

Note: Probability of the student’s blood group not being O = $\frac{3}{10}$

+ $\frac{7}{10}$

= 1.

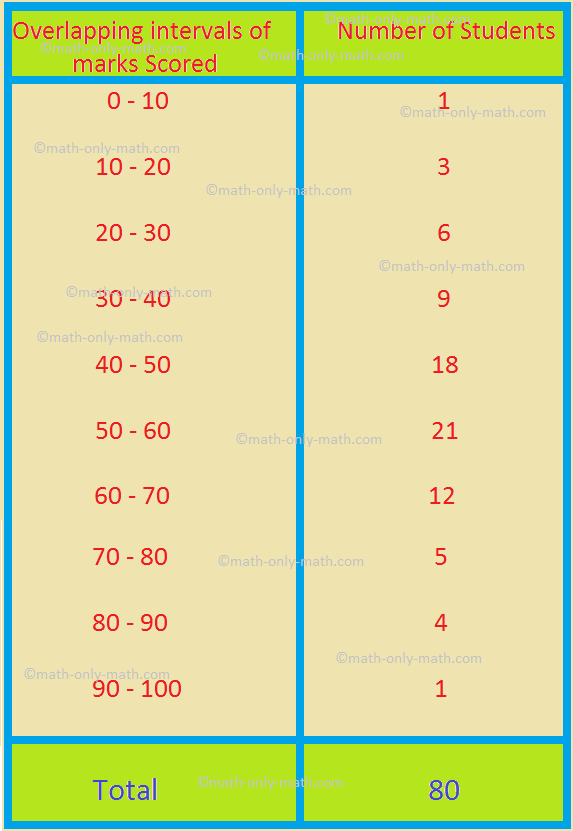
3. In a test of 100 marks, the marks scored by the students of a class are given below.

1Save

A student of the class is selected at random. Find the probability that the student has scored

(i) less than 30

(ii) at least 60

(iii) not less than 80.

Solution:

(i) Total number of trials = 80 [Since there are 80 students all together].

Number of students scoring less than 30 = Cumulative frequency of the interval 20 – 30 = 1 + 3 + 6 = 10.

So, the probability of the student scoring less than 30

= $\frac{Frequency of Favourable Trials}{Total Number of Trials}$

= $\frac{Number of Students Scoring Less than 30}{Total Number of Students}$

= $\frac{10}{80}$

= $\frac{1}{8}$

(ii) Total number of trials = 80.

Number of students scoring at least 60 = Number of students scoring more than or equal to 60

= 12 + 5 + 4 + 1 (= Sum of frequencies of the intervals 60 – 70, 70 – 80, 80 – 90, 90 – 100)

= 22.

So, the required probability = $\frac{Frequency of Favourable Trials}{Total Number of Trials}$

= $\frac{Number of Students Scoring at least 60}{Total Number of Students}$

= $\frac{22}{80}$

= $\frac{11}{40}$

(iii) Total number of trials = 80.

Number of students scoring at not less than 80 = Number of students scoring to least 80

= 4 + 1 (= Sum of frequencies of the intervals 80 – 90 and 90 – 100)

= 5.

Therefore, the required probability = $\frac{Number of Students Scoring not less than 80}{Total Number of Students}$

= $\frac{5}{80}$

= $\frac{1}{16}$

4. A bag contains 8 red balls and some white balls. If the probability of drawing a white ball is half of the probability of drawing a red ball then find the number of white balls in the bag.

Solution:

Let the number of white balls be n.

The number of red balls = 8.

Therefore, the possible number of outcomes = n + 8.

Now, the probability of drawing a white ball = $\frac{n}{n + 8}$

The probability of drawing a red ball = $\frac{8}{n + 8}$

Now, from question,

$\frac{n}{n + 8}$

= $\frac{1}{2}$ ∙ $\frac{n}{n + 8}$

or, n = 4.

So, number of white balls in the bag is 4.

5. A box contains 90 discs numbered 1 to 90. One disc is drawn at random from the box. What is the probability that is bears

(i) a two-digit number

(ii) a perfect square

(iii) a multiply of 5

(iv) a number divisible by 3 and 5.

Solution:

(i) Total number of possible outcomes = 90 (Since the disks are numbered from 1 to 90).

Number of favourable outcomes of the event E

= Number of two-digit numbers from 1 to 90

= 90 – 9 = 81 (Since all are two-digit numbers except 1 to 9)

Therefore, P(E) = $\frac{Number of Favourable Outcomes of the Event E}{Total Number of Possible Outcomes}$

= $\frac{81}{90}$

= $\frac{9}{10}$

(ii) Total number of possible outcomes = 90.

Number of favourable outcomes of the event F

= Number of perfect squares from 1 to 90

= 9 [Since 1, 4, 9, 16, 25, 36, 49, 64 and 81 are perfect squares).

Therefore, by definition, P(F) = $\frac{9}{90}$

= $\frac{1}{10}$

(iii) Total number of possible outcomes = 90.

Number of favourable outcomes of the event G

= Number of multiples of 5 among numbers from 1 to 90

= 18 [Since 5 × 1, 5 × 2, 5 × 3, …., 5 × 18 are multiple of 5).

Therefore, by definition, P(G) = $\frac{18}{90}$

= $\frac{1}{5}$

(iv) Total number of possible outcomes = 90.

Number of favourable outcomes of the event H

= Number of numbers divisible by 3 and 5 from 1 to 90

= Number of numbers divisible by 15 from 1 to 90

= 6 [Since 15 × 1, 15 × 2, 15 × 3, …., 15 × 6 are divisible by 15).

Therefore, by definition, P(H) = $\frac{6}{90}$

= $\frac{1}{15}$

How to Pass Grade 9 with distinctions

One of the most significant accomplishments in your academic career is passing matric. It provides access to a wide range of post secondary options and employment possibilities. Use our best study advice to complete your matriculation, and you’ll succeed with flying colors.

READ => How to get your matric results step by step